计算机中浮点数的存储方式
在计算机中浮点数采用科学记数法
float 4个字节 32位 从高到低依次是:
| 31 | 30-23 | 22-0 |
|---|---|---|
| 符号位 0或1 | 指数位8位 | 小数部分23位 |
举例:十进制的小数20.1如何转成计算机中的存储形式(二进制)呢?
步骤:
- 整数部分和小数部分分别转成二进制
- 整数部分转二进制:除2取余,拿整数部分除2,每次操作记下余数,然后拿商继续除2,直到商为0;最后将每一步求得的余数倒叙排列。
- 小数部分转二进制:乘2取整,拿小数部分即0.xxx乘2,每次操作结果留整数部分,接下来继续拿小数部分乘2,直到小数部分为0;最后将每步求得的整数部分正序排列。
- 移位成标准的科学记数法,即:
- 让指数+127
- 取小数部分位前23位,不足23位后面补0,超过23位只取前23位
实战:
分别将整数和小数部分转成二进制
对于20转二进制:
- 20/2 商10 余0
- 10/2 商5 余0
- 5/2 商2 余1
- 2/2 商1 余0
- 1/2 商0 余1 🔚
所以二进制存储形式:10100
对于0.1转二进制
- 0.1*2 得0.2 整数部分0 接下来拿小数部分0.2继续乘2
- 0.2*2 得0.4 整数部分0 接下来拿小数部分0.4继续乘2
- 0.4*2 得0.8 整数部分0 接下来拿小数部分0.8继续乘2
- 0.8*2 得1.6 整数部分1 接下来拿小数部分0.6继续乘2
- 0.6*2 得1.2 整数部分1 接下来拿小数部分0.2继续乘2
- 0.2*2 得0.4 整数部分0 接下来拿小数部分0.4继续乘2
- 0.4*2 得0.8 整数部分0 接下来拿小数部分0.8继续乘2
- 0.8*2 得1.6 整数部分1 接下来拿小数部分0.6继续乘2
- 0.6*2 得1.2 整数部分1 接下来拿小数部分0.2继续乘2
- 0.2*2 得0.4 整数部分0 接下来拿小数部分0.4继续乘2
- 0.4*2 得0.8 整数部分0 接下来拿小数部分0.8继续乘2
- 0.8*2 得1.6 整数部分1 接下来拿小数部分0.6继续乘2
- 0.6*2 得1.2 整数部分1 接下来拿小数部分0.2继续乘2
- 0.2*2 得0.4 整数部分0 接下来拿小数部分0.4继续乘2
- 0.4*2 得0.8 整数部分0 接下来拿小数部分0.8继续乘2
- 0.8*2 得1.6 整数部分1 接下来拿小数部分0.6继续乘2
- 0.6*2 得1.2 整数部分1 接下来拿小数部分0.2继续乘2
- 0.2*2 得0.4 整数部分0 接下来拿小数部分0.4继续乘2
- 0.4*2 得0.8 整数部分0 接下来拿小数部分0.8继续乘2
- 0.8*2 得1.6 整数部分1 接下来拿小数部分0.6继续乘2
- 0.6*2 得1.2 整数部分1 接下来拿小数部分0.2继续乘2
- 0.2*2 得0.4 整数部分0 接下来拿小数部分0.4继续乘2
- 0.4*2 得0.8 整数部分0 接下来拿小数部分0.8继续乘2
- 0.8*2 得1.6 整数部分1 接下来拿小数部分0.6继续乘2
- 0.6*2 得1.2 整数部分1 接下来拿小数部分0.2继续乘2
- 可以看到已经开始无限循环了 下面的计算省略
所以0.1转成二进制,是一个无限循环小数,即:00011001100110011001100…..
移位成标准记数法
即:10100. 00011001100110011001100110011…. * 2^0
变成:1. 0100 00011001100110011001100110011…*2^4
指数部分处理
4+127=131 ,131转二进制,10000011
小数部分取前23位,不够的末尾补0,超出的截断–这也就是浮点数存在误差的由来
01000001100110011001101(最后这个1是四舍五入来的)
整合最后结果
0(符号位)10000011(指数位)01000001100110011001101(小数位)
0 10000011 01000001100110011001101
转换成16进制:
转换为十六进制(每 4 位一组):
0100 0001 1010 0000 1100 1100 1100 1101 → 0x41A0CCCD
在编译器中验证
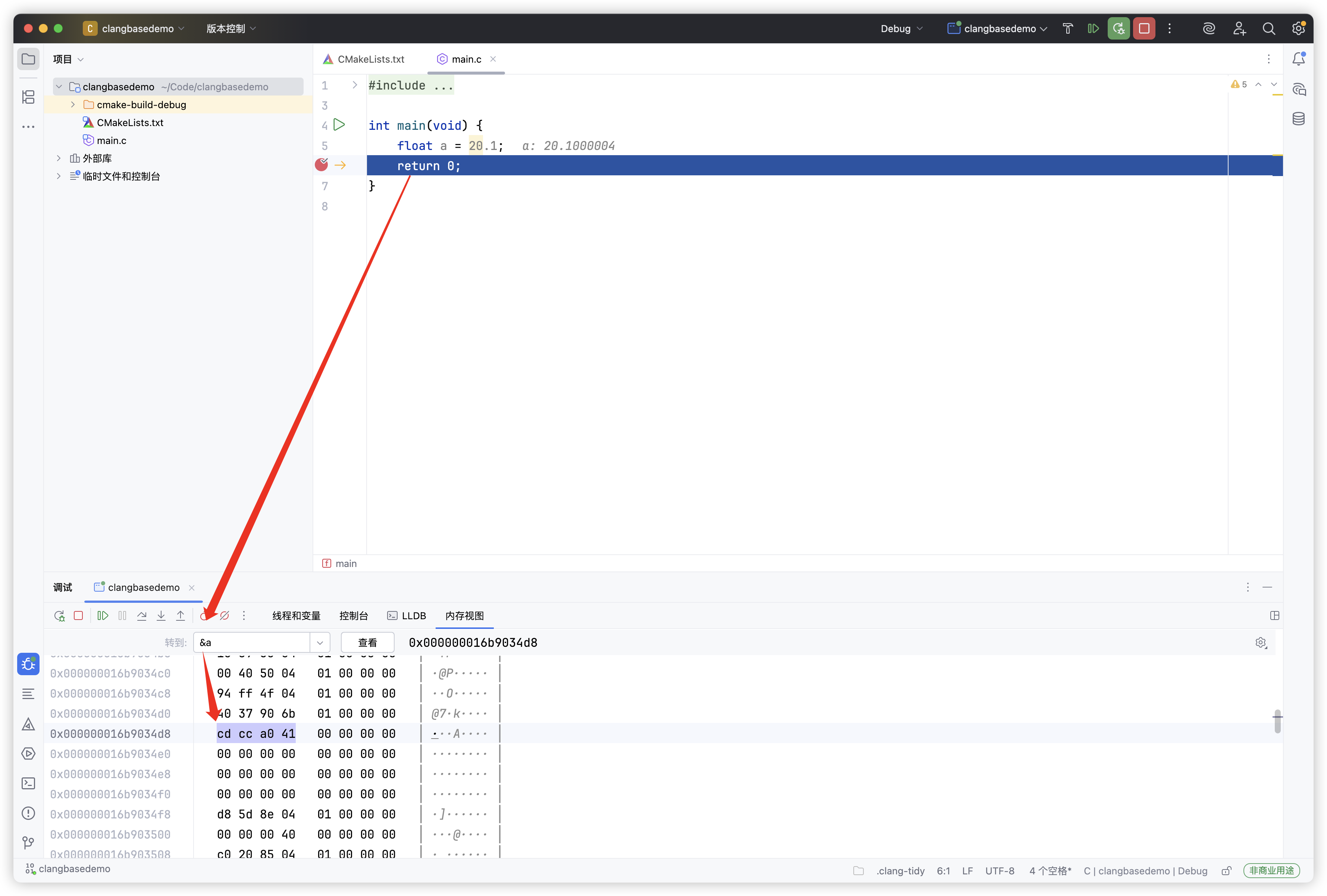
由于是小端存储,所以我们的计算结果其实是对的上的。关于大小端可以看我的这篇博客:C 大端存储与小端存储